1. Introduction

Indoor activities constitute a significant portion of modern life, with studies indicating that individuals spend up to 90 percent of their time indoors. Remote work and digital entertainment have amplified this trend, making building safety more important for life and property protection. Building safety is influenced by a myriad of factors—including the rationality of structural design, construction quality, service life, and external environmental changes. Among these, earthquakes are of particular concern; as sudden and unpredictable natural disasters, they pose a severe threat to structural integrity, with an estimated 50,000 detectable seismic events occurring globally each year, some of which are highly destructive. Consequently, enhancing the seismic resilience of building structures has emerged as a critical research focus.

In recent years, researchers have pursued multiple strategies to improve seismic capacity, such as optimizing building design, incorporating advanced seismic materials and damping devices, and refining structural analysis methods. These approaches improve stability, but traditional design struggles with strong loads, large vibrations, and prolonged effects, which increase costs. To mitigate these challenges, alternative strategies—including base isolation, energy-dissipating damping devices, and active structural control—have been proposed. The Tuned Liquid Damper (TLD), a passive mechanical device typically installed on building roofs, has gained considerable attention for its ability to attenuate structural oscillations by modulating the movement of liquid. Its ease of installation and potential for temporary implementation make it especially attractive for retrofitting existing structures.

Housner's [1] seminal work on a nonlinear TLD model—derived from analyzing the dynamic response of elevated water tanks to seismic ground motions—laid the groundwork for subsequent numerical models that solve the governing equations of liquid motion [2]. As a result, TLDs have been widely adopted in flexible, low-damping structures such as high-rise buildings, towers, and suspension bridges [3, 4]. However, accurately modeling TLD dynamics remains challenging due to the complex nature of building structures. The parameters governing TLD behavior are often difficult to determine and may vary with the building configuration, necessitating continuous adjustment; existing parameter estimation methods frequently struggle to capture these time-varying dynamics with precision [5, 6].

Parameter estimation for the TLD model can be formulated as a nonlinear state estimation problem [7]. Conventional nonlinear estimation methods, such as the Extended Kalman Filter (EKF), rely heavily on model accuracy and require careful design of noise variance—an aspect that is often hindered by limited prior knowledge. Furthermore, the discretization needed for experimental data collection introduces discrepancies between the discrete model and the actual continuous dynamics. To address these issues, risk-sensitive filtering techniques have been developed. Unlike traditional methods that employ a standard quadratic loss function, risk-sensitive approaches use an exponential quadratic loss function that imposes a steeper penalty on larger errors, with the severity modulated by a risk-sensitive parameter [8]. An enhanced variant of this framework—the robust Kalman filter and its extensions [9]—models uncertainty incrementally at each time step by designing the state estimator based on the worst-case model drawn from a fuzzy set defined within the Kullback-Leibler (KL) topology relative to the nominal model. Although several robust EKF variants have been proposed [10], none have fully integrated this paradigm into the EKF framework.

The proposed Robust Extended Kalman Filter exhibits broad applicability beyond TLDs, particularly in vibration control systems that face nonlinear dynamics, model uncertainties, or non-Gaussian noise. In high-rise buildings subjected to wind or seismic loads, REKF could improve real-time estimation of TMD parameters, compensating for structural degradation or sudden load variations. And REKF's adaptive noise covariance adjustment would improve fault-tolerant control of flexible spacecraft or aircraft wings, where sensor noise and high-frequency vibrations often degrade traditional EKF performance. Then for monitoring of bridge or offshore platforms under environmental disturbances, the robustness of REKF to nonstationary noise could refine the damage detection accuracy by isolating true structural resonances from spurious signals.

This paper makes several key contributions: it investigates nonlinear estimation techniques for the TLD system's nonlinear model, develops a suitable vibration response analysis framework, and proposes a robust Extended Kalman Filter (EKF) as a novel solution for enhancing the seismic design of building structures. To validate the effectiveness of the proposed method, the study employs two canonical earthquake signals—the El Centro and Hachinohe waves—and benchmarks the robust EKF against the conventional EKF. The results indicate that the robust EKF yields parameter estimates that closely align with reference values, thereby achieving minimal relative estimation errors.

2. Related Works

Shortly after the introduction of the Wiener [11] and Kalman filters, it became evident that these techniques are vulnerable to modeling errors, which may manifest as spurious signals or disturbances in the system dynamics. Over the past 35 years, numerous methods have been proposed to construct filters that are robust against such uncertainties.

Kassam, Poor, and their collaborators—drawing on Huber's robust statistical framework—introduced an optimal filter selection method formulated as a minimization problem [12]. In this approach, the set of potential system models is characterized by a neighborhood around the nominal model. One "participant" selects the most unfavorable model within this neighborhood, while the other designs the optimal filter for this worst-case scenario. Although conceptually straightforward, implementing minimization-based filtering is challenging because it requires specifying both the allowable neighborhood and the loss function to be minimized. Early successes in this vein involved designing Wiener filters for neighborhoods defined by contaminated models or restricted power spectral bands; however, these efforts eventually plateaued, spurring further research into robust filtering from alternative perspectives.

In the 1980s, a distinct class of robust filters was developed based on the minimization of risk-sensitive and $H_{\infty }$ performance criteria. These methods aim to mitigate large errors—even those that are unlikely under the nominal model. For instance, risk-sensitive filters replace the standard quadratic loss function of least-squares filtering with an exponential quadratic function that severely penalizes large deviations.

Nonetheless, neither $H_{\infty }$ nor risk-sensitive filters explicitly account for errors in the model dynamics [13]. Recognizing the importance of these dynamic errors, researchers in the early 2000s revisited the concept of least-squares filtering, now incorporating modeling errors as disturbances in the state-space dynamics.

Building on efforts initiated by Hansen, Sargent, and others, risk-sensitive filtering was reinterpreted from the perspective of minimizing the worst-case limit. In this reformulation, modeling uncertainty is quantified by specifying a tolerance for the relative entropy between the actual system and the nominal model. A fixed tolerance level, reflecting the modeler's confidence in the nominal model, defines a "model sphere" to which the minimization approach of Kassam and Poor can be applied [14].

The robust filtering formulation based on relative entropy constraints offers several attractive features. Relative entropy serves as a natural measure of model mismatch and is frequently employed in statistical techniques such as Expectation-Maximization iterations. Moreover, foundational studies by Chentsov and Amari have shown that the statistical model manifold possesses non-Riemannian differential geometric structures characterized by two dual connections associated with relative entropy and its reverse.

Recent work has further demonstrated that the minimization problem for Wiener and Kalman filters under relative entropy constraints can be reformulated as a risk-sensitive filter [15], thereby providing a novel interpretation of these filters. A key difference between earlier research and the present study is that we impose separate relative entropy constraints on each time increment of the model rather than a single constraint over the entire system. This modification is motivated by the observation that a single constraint allows the maximizer to concentrate nearly all of the mismatch budget on the component most susceptible to uncertainty, potentially leading to overly pessimistic conclusions. In practice, modelers distribute their efforts uniformly across time steps, making a fixed uncertainty tolerance for each increment more meaningful.

Tuned Liquid Damper (TLD) technology plays a critical role in reducing building vibrations at a relatively low cost. A comprehensive understanding of TLD dynamic behavior is essential for future design improvements. The dynamic characteristics of a TLD are modeled using the Housner model, which describes the relative displacement of the water (denoted to as d) as follows:

where u is the tank's base acceleration ; $\xi$ is the ratio of damping and $\omega$ is the water's oscillation frequency. The goal is to infer the model parameters by measuring the reaction force applied to the bottom of the tank.

where the total mass of water $m_t$is known. The parameter $\xi$ is the restraining springs to the total mass of water in the tank. $\beta$ is adjustable using a baffle and assumed to be a known constant .

Therefore, the parameters to be estimated are $\beta$ and $\omega$, the latter of which can be viewed as state components. For the sake of the consequent estimation process and the existence of the process and measurement noise in practice, the Housner model can be written as follows:

Accordingly, the problem becomes to estimate the state of the nonlinear state model in (3)-(4). Here, we assume the process noise vand the measurement noise ware white Gaussian noises(WGN) with variances Qand R, respectively. The process variance Qis a diagonal matrix such that:

Note that we choose the first two components of the diagonal (corresponding to $\dot{d}$ and $d$) with high magnitude to ensure variability over time, while the other two components (relative to $\beta$ and $\omega$) are selected with small value so that the estimated parameters change a little over time. In plain words ${\sigma }_3$ and ${\sigma }_4$ tune the a priori information about the changing rate of $\beta$ and $\omega$ in the stochastic hypermodel(15). Then, the initial state $x_0$ is modeled as a Gaussian random vector with mean ${\hat{x}}_0$ and variance $V_0$:

As the data is gathered over a defined sampling interval, the initial step involves discretizing the state equations. To achieve this, the fourth-order Runge-Kutta method is utilized. However, this procedure may introduce a discrepancy between the nominal model and the true model. There is inherent model uncertainty between the real and nominal models. To address this issue, a robust Kalman filter estimation method will be used.

3. Methods

However, in practical scenarios, there is often a mismatch between the nominal model and the actual model. This mismatch arises mainly due to two factors. First, model parameters are subject to uncertainties, such as the true structure of $\text{f}(\cdot )$ and the variance of the noise. Second, the physical model is naturally described using a continuous-time framework.

Literature shows that traditional Kalman filters are sensitive to model uncertainty. In Section 2, we introduce a robust filtering approach that discretizes the TLD model while accounting for discretization-induced errors, thereby establishing an improved framework.

Based on this foundation, the robust extended Kalman filter (REKF) is employed in this study to estimate the nonlinear model. The subsequent section delineates the discrete state-space representation of the TLD system and its integration within the REKF framework. Specifically, we consider the following discrete-time state-space model:

where $x_t\in {ℝ}^n$ denotes the state process, $u_t\in {ℝ}^q$ represents the known input, and $v_t\in {ℝ}^m$ is WGN all of which corresponse to the time step t. Our goal objective is to recursively estimate the state $x_{t+1}$ from the observed process $y_t\in {ℝ}^p$ . If the functions $f(\cdot )$ and $h(\cdot )$ are linear, the estimation problem admits a well-established solution via the Kalman filter, conversely, if either function is nonlinear, the extended Kalman filter (EKF) is employed to address the estimation task.

where $Y_{t-1}=\left\{y_s,0\le s\le t-1\right\}$.The filter uses the nominal model (7) at each step, linearized around the previous estimate. It is well known that the evolution of the estimate for this problem is:

where ${\hat{x}}_{t\mid t}$ and ${\hat{x}}_t$ represent the estimated values of ${\hat{x}}_t$ given $Y_t$ and $Y_{t-1}$, and $L_t$ is the filter gain.

Since the Extended Kalman Filter (EKF) is being used, the model must be linearized. However, this linearization introduces extra model discrepancy. To address this, a robust approach is introduced to enhance the estimation performance, taking into account the errors introduced by the linearization process. The method starts by considering the model in equation (7), where the state equation is linearized with respect to ${\hat{x}}_{t\mid t}$, and the measurement equation is linearized with respect to ${\hat{x}}_t$:

where,

Let $z_t={\left[x_{t+1}^T{y}_t^T\right]}^T$. We assume that the noise $v_t$ affects all components of the dynamic observations in equations (7) and (11), and therefore the covariance matrix is given as:

The covariance matrix is ensured to be positive definite. To develop the robust filter, a minimax approach is utilized on the linearized model (11), as proposed in recent studies [15, 16]. Let ${\varphi }_t\left(z_t\mid x_t\right)$ denote the actual transition probability density of $x_t$ given $z_t$. Here, $\widetilde{{\varphi }_t}$ is not necessarily Gaussian. The mismatch between the probability densities ${\varphi }_t$ and $\widetilde{{\varphi }_t}$ is measured using the Kullback-Leibler (KL) divergence:

Next, we assume that $\widetilde{{\varphi }_t}$ belongs to $B_t$, that is, approximately a ball of the nominal density.

where $c_t>0$ represents the tolerance specified for each time step. The tolerance is measured by the KL divergence, quantifying the model mismatch budget between the nominal model and the actual model at time t. By considering a max-min optimization problem, the gain in Equation (9) is computed robustly $L_t$ :

where $G_t$ is the set of all ${\tilde{\varphi }}_t\in B_t$ bounded estimators in (15) Therefore, the gain calculation here refers to the worst-case description. Assuming the prior probability density of $x_t$ conditioned on the observations $Y_{t-1}$:

The worst-case solution to (15) follows a Gaussian distribution [5],while its variance changes. Given that the worst-case (linearized) model is Gaussian and the estimator solution of (15) is Bayesian, the estimator for the original model is provided by (9), where the filtering gain is now:

here,

where ${\theta }_t>0$ is the unique solution to $\gamma (P_{t+1},{\theta }_t)=c_t$ and $\gamma (P,\theta )=\frac{1}{2}logdet\left(I-\theta P\right)+tr\left[{\left(I-\theta P\right)}^{-1}-I\right]$. However, since the variance of ${\varphi }_t$ differs from that of ${\tilde{\varphi }}_t$, the filtering gain is not the same as the standard gain. Therefore, this robust approach must be used to determine the gain for the linearized version of the model in (7). The overall process is similar to the EKF, except for the presence of $V_t$, which requires the computation of ${\theta }_t$ . This computation must be carried out numerically, as no closed-form solution exists.

4. Experiments

Real-time hybrid simulation technology is employed to evaluate the Tuned Liquid Damper (TLD) system. As illustrated in Figure 1, when a seismic signal is applied to the structure, the relative displacement between the structure's top and the TLD system is transmitted as input to the shaking table, thereby enabling the measurement of the relative acceleration at the tank's bottom via an accelerometer.

Figure 1 Real-time hybrid simulation technology schematic diagram.

Figure 2 Laboratory water tank unit.

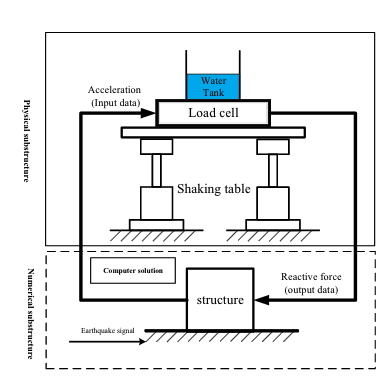
Figure 2 depicts the test configuration, which comprises a water tank mounted on a shaking table with dimensions of 0.8 × 0.8 × 0.268 m (length × width × height). The seismic inputs include two classic earthquake records—the El Centro and Hachinohe waves. To elucidate the impact of seismic excitation characteristics on TLD parameter estimation, a comparative analysis was conducted using the El Centro wave and Hachinohe wave, two representative ground motions with distinct spectral and non-stationary features. Key differences are summarized as follows, El Centro waves dominant low-frequency components (0.5–5 Hz), peak ground acceleration (PGA) of 0.35g, and energy concentrated within the initial 10 seconds, exhibiting weak non-stationarity. Hachinohe waves broadband frequency content (0.2–10 Hz), PGA of 0.25g, prolonged duration with evenly distributed energy, and trong non-stationarity due to multiple high-frequency pulses.

The relative acceleration and reaction force signals collected during the test are filtered to reduce noise and subsequently compiled into a dataset for model parameter estimation, with a sampling interval of $T_s=0.01s$ corresponding to the variables $u$ and $y$ introduced in Section 2.

Initially, the experimental data were processed using both the Extended Kalman Filter (EKF) and the Unscented Kalman Filter (UKF), two widely used methods for nonlinear state estimation. The UKF, which more accurately approximates the state distribution, is particularly effective in handling pronounced nonlinearity and serves as a useful benchmark in this study.

The constant model parameters were set as $\xi$ = 0.005 and $m_t$ = 171.51 kg, while the reference values derived from the Housner model were $\beta$ = 0.613 and $\omega$ = 5.479 rad/s.

Two datasets were evaluated under different conditions: one assuming approximate prior knowledge of the initial values for $\beta$ and $\omega$, and the other initializing these parameters at their lower bounds. Root Mean Square Error (RMSE) was used as the primary metric for assessing estimation accuracy.

For the prediction frameworks, the initial state conditions were specified as:

with the initial covariance matrix defined as $v_0=\mathrm{diag}(1,1,0.001,0.1)$. The results are shown in Figures 3, 4, 5 and 6.

Figure 3 Comparison of Beta estimates for the El Centro wave dataset using EKF and UKF at $x_0\left(1\right)$ .

Figure 4 Comparison of Beta estimates for the El Centro wave dataset using EKF and UKF at $x_0\left(2\right)$.

Figure 5 Comparison of Omega estimates for the El Centro wave dataset using EKF and UKF at $x_0\left(1\right)$.

Figure 6 Comparison of Omega estimates for the El Centro wave dataset using EKF and UKF at $x_0\left(2\right)$.

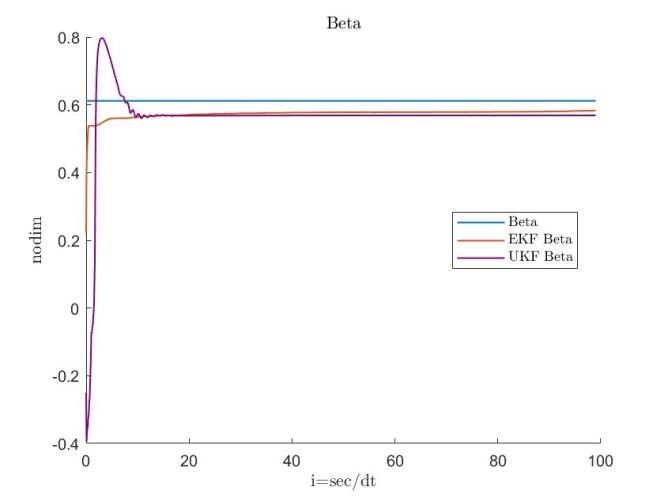
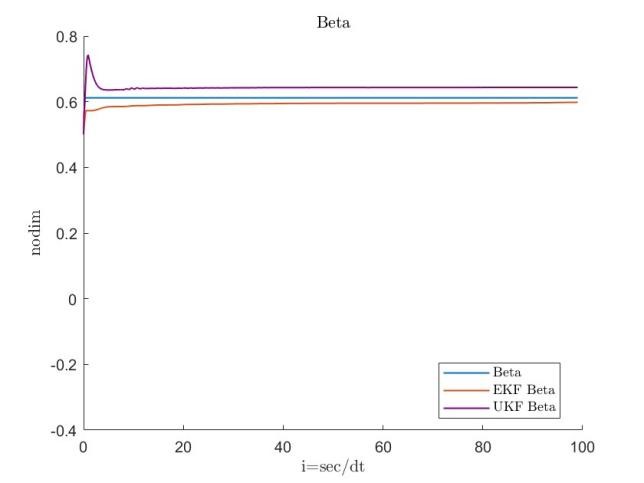
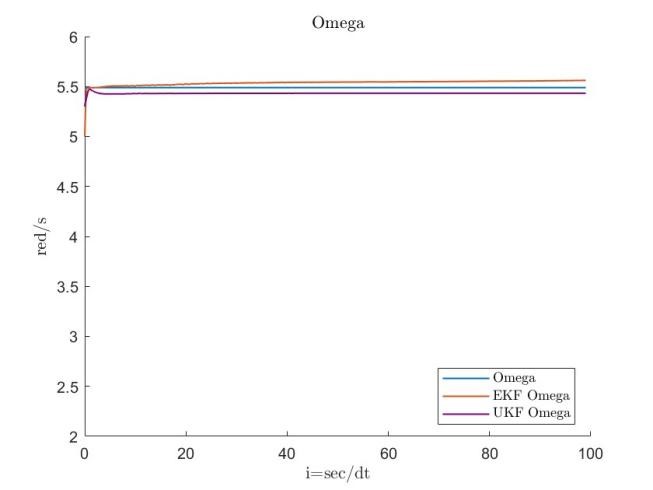
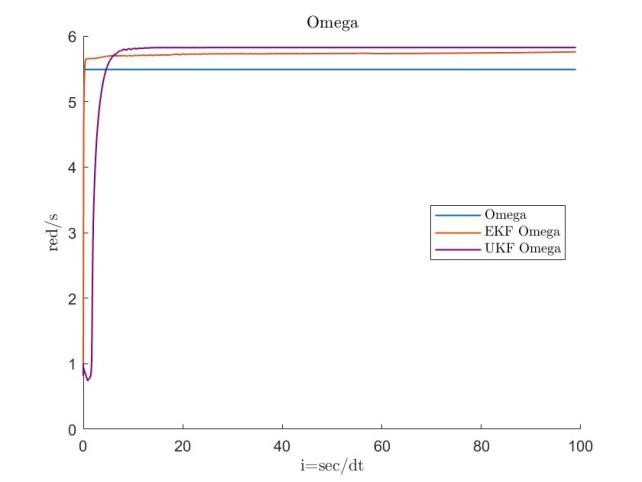
For the Hachinohe wave dataset, $v_0$ was set to $\mathrm{diag}(1,1,0.002,0.15)$. Adjustments to the process variance matrix for $\beta$ and $\omega$ were made depending on whether the initial state estimates were assumed to be close to the reference values.

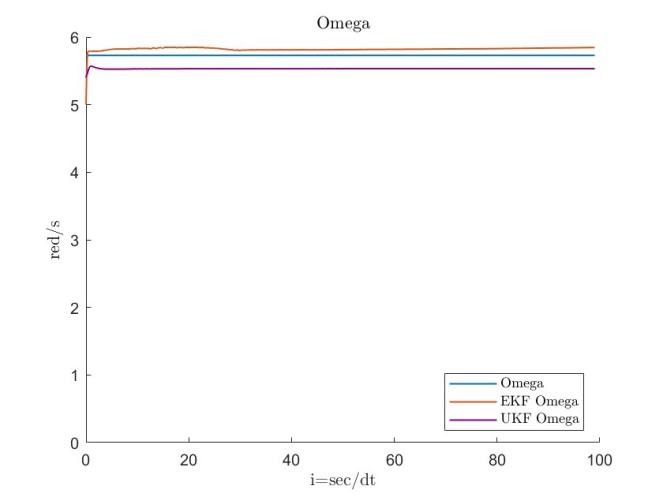
The results presented in Figures 7, 8, 9 and 10 indicate that the EKF yields stable estimates with lower errors compared to the UKF, prompting further refinement of the EKF approach. All simulations assume an output noise variance of $R=1$ , and the tolerance parameter is initiated at $c_0=0.001$.

Figure 7 Comparison of Beta estimates for the Hachinohe wave dataset using EKF and UKF at $x_0\left(1\right)$.

Figure 8 Comparison of Beta estimates for the Hachinohe wave dataset using EKF and UKF at $x_0\left(2\right)$.

Figure 9 Comparison of Omega estimates for the Hachinohe wave dataset using EKF and UKF at $x_0\left(1\right)$.

Figure 10 Comparison of Omega estimates for the Hachinohe wave dataset using EKF and UKF at $x_0\left(2\right)$.

Figure 11 Comparison of Beta estimates for the El Centro wave dataset using EKF and REKF at $x_0\left(1\right)$.

Figure 12 Comparison of Beta estimates for the El Centro wave dataset using EKF and REKF at $x_0\left(2\right)$.

Figure 13 Comparison of Omega estimates for the El Centro wave dataset using EKF and UKF at $x_0\left(1\right)$.

Figure 14 Comparison of Omega estimates for the El Centro wave dataset using EKF and UKF at $x_0\left(2\right)$.

Figure 15 Comparison of Beta estimates for the Hachinohe wave dataset using EKF and REKF at $x_0\left(1\right)$.

Figure 16 Comparison of Beta estimates for the Hachinohe wave dataset using EKF and REKF at $x_0\left(2\right)$.

Figure 17 Comparison of Omega estimates for the Hachinohe wave dataset using EKF and UKF at $x_0\left(1\right)$.

Figure 18 Comparison of Omega estimates for the Hachinohe wave dataset using EKF and UKF at $x_0\left(2\right)$.

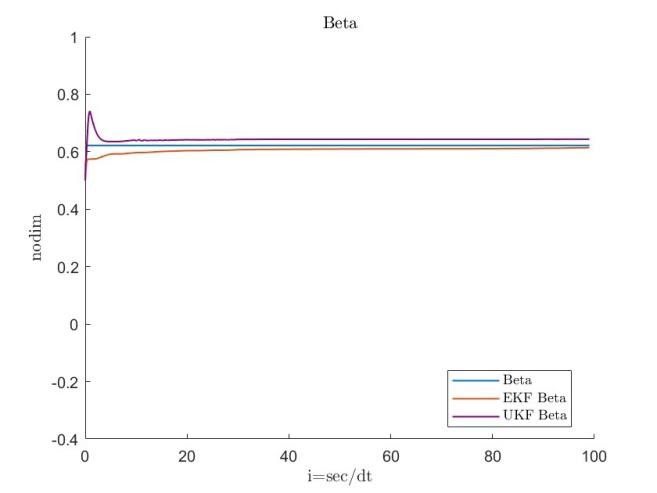
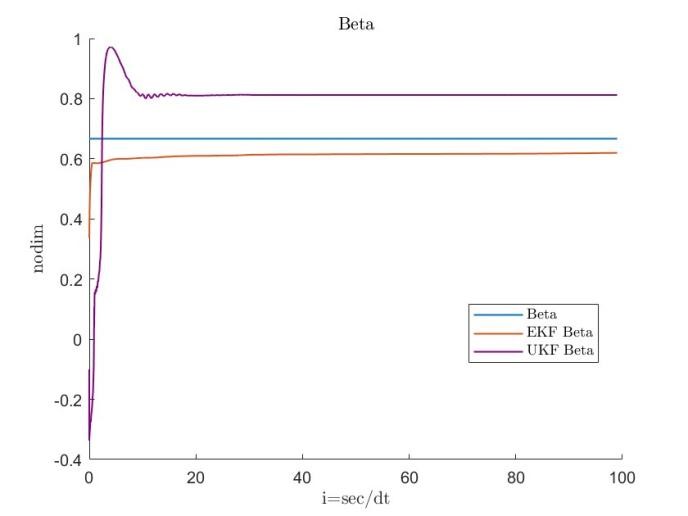
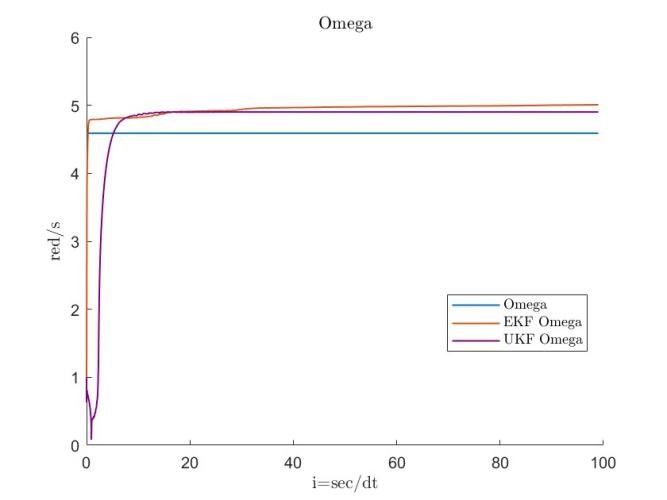
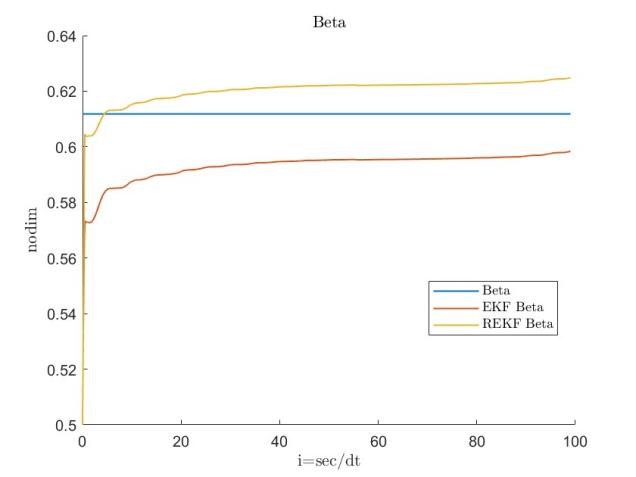
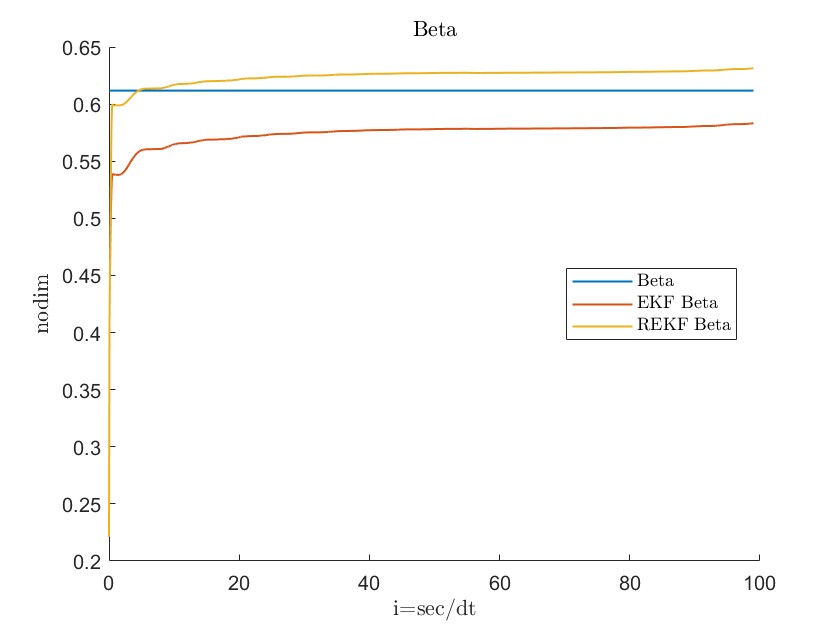
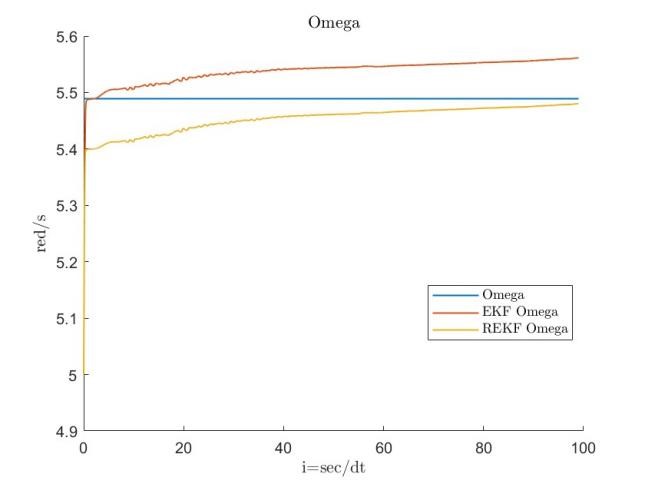
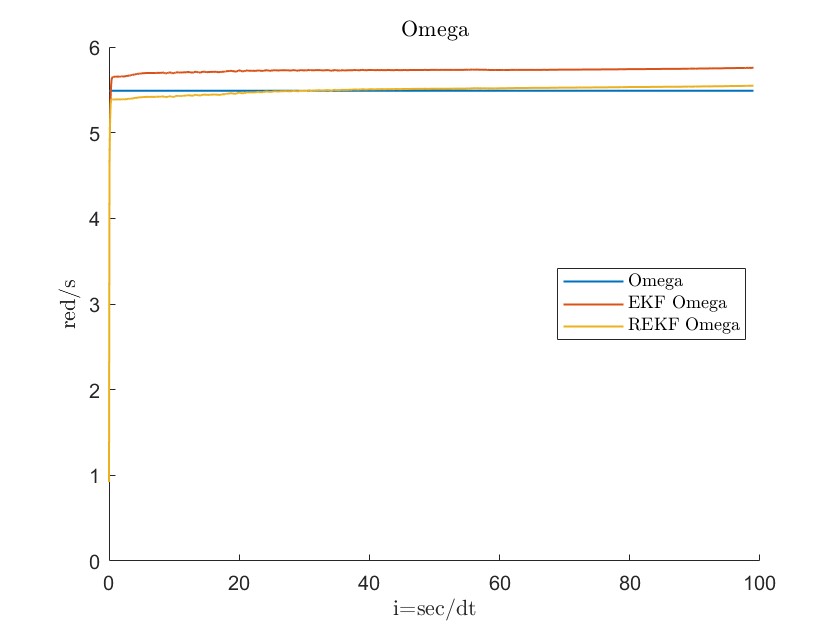
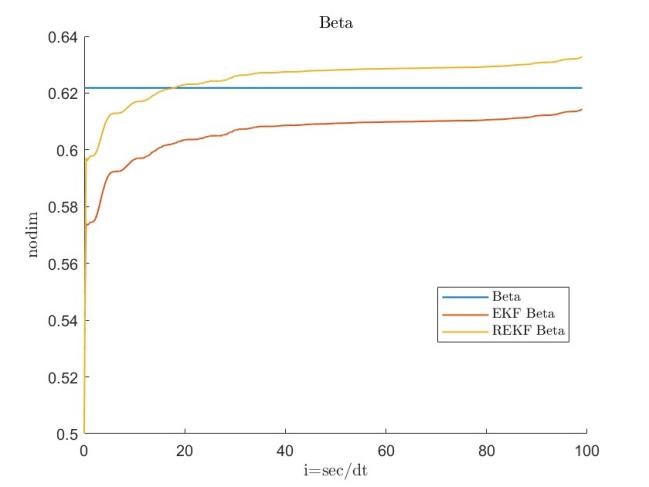
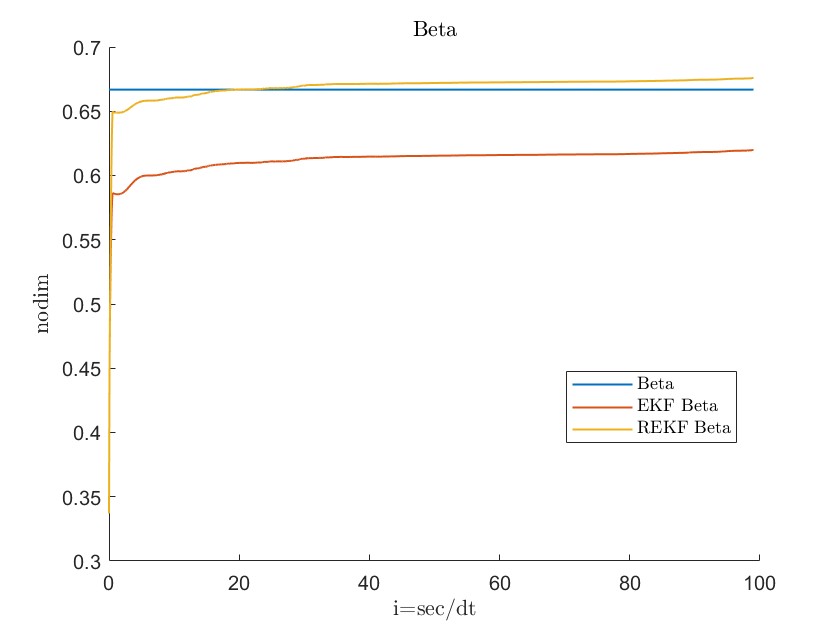
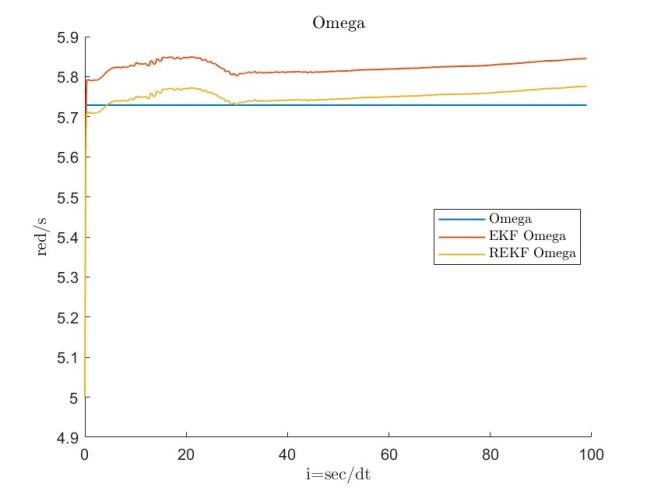
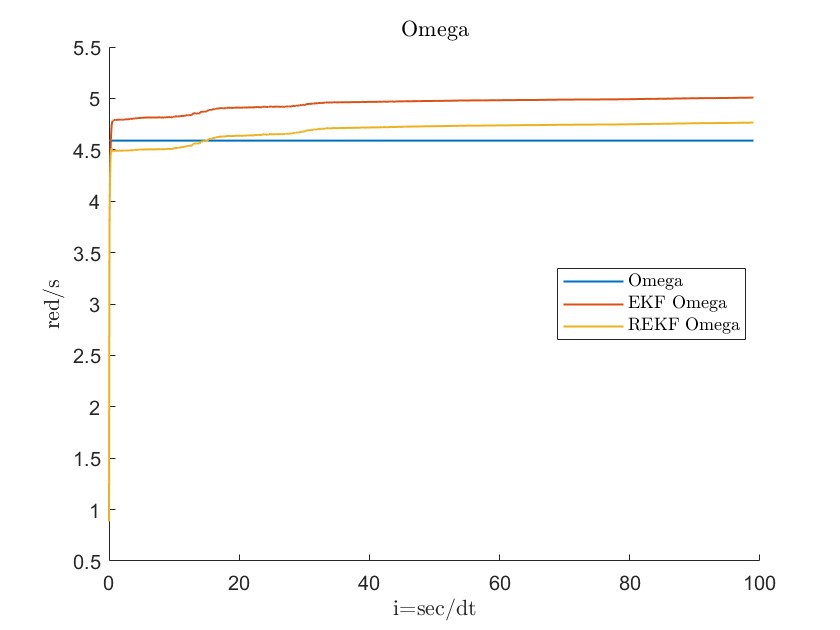
During the initial phase, limited knowledge of the true values for $x_3$ and $x_4$ can lead to inaccuracies in the linearization process. The initial state error covariance matrix $V_0$, the process covariance matrix $Q$, and the estimation results for both datasets are provided below, with RMSE serving as the primary error metric.

Figures 11, 12, 13, 14, 15, 16, 17 and 18 demonstrate that the robust extended Kalman filter (REKF) accurately identifies the parameters $\beta$ and $\omega$ for both datasets. Moreover, the REKF outperforms the standard EKF: in 40 out of 100 trials, the REKF results converge to the reference values. Once the true values are attained, the estimates remain close to these references. Specifically, using the REKF method, the relative error for $\beta$ remains below 1percent and for $\omega$ below 3 percent, whereas the standard EKF exhibits relative errors of 4 percent for $\beta$ and 19 percent for $\omega$. These results substantiate that the REKF provides superior performance over the standard EKF under both sets of initial conditions.

5. Conclusion

This paper addresses the nonlinear modeling of Tuned Liquid Dampers (TLD) and presents a parameter estimation approach based on a Robust Extended Kalman Filter (REKF). The proposed method mitigates uncertainties arising from model discretization errors and limited knowledge of noise processes. By incrementally representing these uncertainties, the REKF effectively captures the dynamic behavior of TLD systems, as demonstrated through experimental validation. Experiments employing classical seismic records, namely the El Centro and Hachinohe waves, were conducted under two distinct initial conditions. The results indicate that, although the REKF requires slightly more computational time than the standard Extended Kalman Filter (EKF), it substantially enhances parameter estimation accuracy and robustness. Furthermore, the REKF exhibits stability and adaptability under varied experimental conditions, thereby providing reliable technical support for future TLD dynamic modeling and seismic design. By introducing an improved robust nonlinear estimation technique, this study offers a novel approach to parameter estimation and vibration response analysis for TLD models, laying a critical foundation for optimizing the seismic performance of complex building structures.